Implementing the transcendental functions in Ivy

Towards the end of 2014, in need of pleasant distraction, I began writing, in Go, my second pseudo-APL, called Ivy. Over the years, Ivy's capabilities expanded to the point that it's now being used to do things such as to design floating-point printing algorithms. That was unexpected, doubly so because among the set of array languages founded by APL, Ivy remains one of the weakest.

Also unexpected was how the arrival of high-precision floating point in Go's libraries presented me with some mathematical challenges. Computing functions such as sine and cosine when there are more bits than the standard algorithms provide required polishing up some mathematics that had rusted over in my brain. In this article, I'll show the results and the sometimes surprising paths that led to them.

First I need to talk a bit more about Ivy itself.

For obvious reasons, Ivy avoids APL's idiosyncratic character set and uses ASCII tokens and words, just as in my previous, Lisp-written pseudo-APL back in 1979. To give it a different flavor and create a weak but valid justification for it, from the start Ivy used exact arithmetic, colloquially big ints and exact rationals. This made it unusual and a little bit interesting, and also meant it could be used to perform calculations that were clumsy or infeasible in traditional languages, particularly cryptographic work. The factorial of 100, in Ivy (input is indented):

  !100      93326215443944152681699238856266700490715968264381621468592963895217599993229915608941463976156518286253697920827223758251185210916864000000000000000000000000

Or perhaps more surprising:

    0.5

1/2

Ivy also became, due to the work of Hana Kim and David Crawshaw, the first mobile application written in Go. I take no credit for that. The iOS version is long gone and the Android version is very old, but that situation might change before long.

For those who don't know the history and peculiarities of APL, it's worth doing your own research; that education is not the purpose of this article. But to make the examples comprehensible to those sadly unfamiliar with it, there are a few details of its model one should understand to make sense of the Ivy examples below.

First, every operator, whether built-in or user-programmed, takes either one argument or two. If one, the operator precedes the argument; if two, the arguments are left and right of the operator. In APL, these are called monadic and dyadic operators. Because Ivy was written based on my fading memory of APL, rather than references, in Ivy they are called unary and binary. Some operators work in either mode according to the surrounding expression; consider

    1 - 2  # Binary: subtraction

-1

    - 0.5  # Unary: negation

-1/2

The second detail is that values can be scalars or they can be multidimensional vectors or matrices. And the operators handle these in a way that feels deeply natural, which is part of why APL happened:

    4 5 6 - 2

2 3 4

    4 5 6 - 1 2 3

3 3 3

Compare those expressions to the equivalent in almost any other style of language to see why APL has its fans.

Finally, because the structure of APL expressions is so simple with only two syntactic forms of operators (unary and binary), operator precedence simply does not exist. Instead, expressions are evaluated from right to left, always (modulo parentheses). Thus

3 * 4 + 5

evaluates to 27 because it groups as 3 * (4+5): every operand is maximal length, traveling left, until an operator arrives. In most languages, the usual precedence rules would instead group this as (3*4) + 5.

Enough preamble.

Ivy was fun to write, which was its real purpose, and there were some technical challenges, in particular how to handle the fluid typing, with things changing from integers to fractions, scalars to vectors, vectors to matrices, and so on. I gave a talk about this problem very early in Ivy's development, if you are interested. A lot has changed since then but the fundamental ideas persist.

Before long, it bothered me that I couldn't calculate square roots because Ivy did not handle irrational numbers, only exact integers and rationals. But Robert Griesemer, who had written the math/big library that Ivy used, decided to tackle high-precision floating point. This was important not just for Ivy, but for Go itself. The rules for constants in Go require that they can be represented to high precision in the source code, much more so than the usual 64-bit variables we are used to. That property allowed constant expressions involving floating-point numbers to be evaluated at compile time without losing precision.

At the time, the Go toolchain was being converted from the original C implementation to Go, and the constant evaluation code in the original compiler had some problems. Robert decided, with his usual wisdom and tenacity, to build a strong high-precision floating-point library that the new compiler could use. And Ivy would benefit.

By mid-2015, Ivy supported floats with lots of bits. Happiness ensued:

sqrt 2

1.41421356237

)format '%.50f'

sqrt 2

1.41421356237309504880168872420969807856967187537695

Time to build in some helpful constants:

pi

3.14159265358979323846264338327950288419716939937511

e

2.71828182845904523536028747135266249775724709369996

Internally these constants are stored with 3000 digits and are converted on the fly to the appropriate precision, which is 256 bits by default but can be set much bigger:

)prec 10000       # Set the mantissa size in bits

)format '%.300f'  # Set the format for printing values

pi

3.141592653589793238462643383279502884197169399375105820974944592307816406286208998628034825342117067982148086513282306647093844609550582231725359408128481117450284102701938521105559644622948954930381964428810975665933446128475648233786783165271201909145648566923460348610454326648213393607260249141274

Now things get harder.

Square root is easy to calculate to arbitrary precision. Newton's method converges very quickly and we can even use a trick to speed it up: create the initial value by halving the exponent of the floating-point argument.

But what about sine, cosine, exponential, logarithm? These transcendental functions are problematic computationally. Arctangent is a nightmare.

When I looked around for algorithms to compute these functions, it was easy to find clever ways to compute accurate values with 64-bit floating-point (float64) inputs, but that was it. I had to get creative.

What follows is how I took on programming high-precision transcendental functions and their relatives. It was a lot of fun and I uncovered some fascinating things along the way.

Disclaimer: Before going further, I must admit that I am not an expert in numerical computation. I am not an expert in analysis. I am not an expert in calculus. I have just enough knowledge to be dangerous. In the story that follows, if I say something that's clearly wrong, I apologize in advance. If you see a way I could have done better, please let me know. I'd love to lift the game. I know for a fact that my implementations are imperfect and can get ratty in the last few bits. And I cannot state anything definitive about their error characteristics. But they were fun to puzzle out and implement.

In short, here follows the ramblings of a confessed amateur traversing unfamiliar ground.

The easiest transcendental functions to provide are sine, cosine, and exponential. These three are in fact closely related, and can all be computed well using their Taylor series, which converge quickly even for large values. Here for instance is the Taylor series (actually a Maclaurin series, since we start at 0) for exponential (thanks to Wikipedia—which, by the way, I support financially and hope you do too—for the screen grab of these equations):

Those factorials in the denominator make this an effective way to compute the exponential. And the sine and cosine series are closely related, taking alternate (sine odd, cosine even) terms from the exponential, with alternating signs:

Euler's famous identity 

might help explain why these three functions are related. (Or not, depending on your sensibilities.)

The challenge with sine and cosine is not the calculation itself, but the process of argument reduction. Because these functions are periodic, and because small values of the argument do better in a Taylor series, it is a good idea to "reduce" or unwind the argument into the range of 0 to 2𝛑. For very large values, this reduction is hard to do precisely, and I suspect my simplistic code isn't great.

For tangent, rather than fight the much clumsier Taylor series, I just computed sin(x) and cos(x) and returned their quotient, with care.

That process of taking existing implementations and using identities to build a new function was central to how Ivy eventually supported complex arguments to these functions as well as hyperbolic variants of them all. For example, for complex tangent, we can use this identity:

tan(x+yi) = (sin(2x) + i sinh(2y))/(cos(2x) + cosh(2y))

Here sinh is the hyperbolic sine, which is easy to compute given the exponential function or by just taking the odd terms of the Taylor series for exponential, while cosh takes the even terms. See the pattern?

Next up we have the inverse functions arcsine (asin) and arccosine (acos). They aren't too bad but their Taylor series have poor convergence when the argument is near ±1. So we grub around for helpful identities and come up with two:

asin(x) = atan(x/sqrt(1-x²))

acos(x) = π/2 - asin(x)

But that means we need arctangent (atan), and its Taylor series has awful convergence for x near 1, whose result should be the entirely reasonable π/4 or 45 degrees. An experiment showed that using the Taylor series directly at 1.00001 took over a million iterations to converge to a good value. We need better.

I did some more exploration and in one of my old schoolbooks I found this identity:

atan(x) = atan(y) + atan((x-y)/(1+xy))

In this identity, y is a free variable! That allows us to do better. We can choose y to have helpful properties. Now:

tan(π/8) = √2-1

or equivalently,

atan(√2-1) = π/8

so we can choose y to be √2-1, which gives us

atan(x) = π/8 + atan((x-y)/(1+xy))   # With y = √2-1

so all we need to compute now is one arctangent, that of (x-y)/(1+xy). The only concern is when that expression nears one. So there are several steps.

First, atan(-x) is -atan(x), so we take care of the sign up front to give us a non-negative argument.

Next if |1-x|< 0.5, we can use the identity above by recurring to calculate atan((x-y)/(1+xy)) with y=√2-1. It converges well.

If x is less than 1 the standard series works well:

atan(x) = x - x³/3 + x⁵/5 - x⁷/7 + ...

For values above 1, we use this alternate series:

atan(x) = +π/2 - 1/x + 1/3x³ -1/5x⁵ + 1/7x⁷ - ...

Figuring all that out was fun, and the algorithm is nice and fast. (Values troublesomely close to 1 are picked off by the identity above.)

So now we have all the arc-trig functions, and in turn we can do the arc-hyperbolics as well using various identities.

With trigonometry out of the way, it's time to face logarithms and arbitrary powers. As with arctangent, the Taylor series for logarithm has issues. And we need logarithms to calculate arbitrary powers: using Ivy's notation for power,

x ** y

is the same as

e ** y*log x

That's the exponential function, which we have implemented, but this necessary rewrite relies on the logarithm of x.

(If the power is an integer, of course, we can just use exact multiplication, with a clever old algorithm that deserves another viewing:

# pow returns x**exp where exp is an integer.

op x pow exp =

z = 1

:while exp > 0

:if 1 == exp&1

z = z*x

:end

x = x*x

exp = exp>>1

:end

z

.5 pow 3

1/8

That loop is logarithmic (ha!) in multiplications. It is an exercise for the reader to see how it works. If the exponent is negative, we just invert the result.)

The Taylor series for log(x) isn't great but if we set x=1-y we can use this series:

log (1-y) = -y - y²/2 - y³/3 ...

It converges slowly, but it does converge. If x is big, the convergence is very slow but that's easy to address. Since log(1/x) is -log(x), and 1/x is small when x is large, for large x we take the inverse and recur.

There's more we can do to help. We are dealing with floating-point numbers, which have the form (for positive numbers):

mantissa * 2**exponent

and the mantissa is always a value in the close/open range [0,0.5), so its series will converge well. Thus we rewrite the calculation as:

log(mantissa * 2**exponent) = log(mantissa) + log(2)*exponent

Now we have a good mantissa we can use in the series and a working exponential function. All that's missing is an accurate value for log(2).

When I was doing this work, I spent a long but unsuccessful time looking for a 3,000-digit accurate value for log(2). Eventually I decided to use Ivy itself, or at least the innards, to compute it. In fact I computed 10,000 digits to be sure, and was able to spot-check some of the digits using https://numberworld.org/digits/Log(2)/, which had sample sparse digits, so I was confident in the result.

The calculation itself was fun. I don't remember exactly how I did it, but looking at it now one way would be to compute

log(0.5) = -log 2

with the series above. With x=0.5, 1-x also equals 0.5 so

log(2) = -log (0.5) = -(-0.5 - 0.5²/2 - 0.5³/3...)

and that converges quickly. The computation didn't take long, even for 10,000 digits.

I then saved the result as a constant inside Ivy, and had all that was needed for x**y.

Finally, if we need the logarithm of a negative or complex number, that's easy given what we've already built:

log(x) = log(|x|) * phase(x)

To compute the phase, we use the arctangent calculation we worked out before.

And with that, Ivy had square roots, trigonometry, hyperbolic trigonometry, logarithms and powers, all for the whole complex plane. That was it for quite a while.

But come late 2025, I decided to fill one gap that was bothering me: The gamma function 𝚪(z), which is defined by the integral

This function has many fascinating properties, but there are three that matter here. First is that if you play with that integral by parts you can discover that it has a recurrence relation

𝚪(z+1) = z𝚪(z)

which is a property shared by the factorial function:

z+1! = z!z

Because of this, the gamma function is considered one way to generalize factorial to non-integers, in fact to the whole complex plane except for non-positive integers, which are its poles. For real(z) < 0, we can (and do) use the identity

𝚪(z) = 𝛑/(sin(z𝛑)*𝚪(1-z))

It works out that for integer values,

𝚪(z+1) = z!

which means, if we so choose, we can define factorial over the complex plane using

z! = 𝚪(z+1)

APL and Ivy both do this.

The second property, besides being easy to evaluate for integer arguments because of the relation with factorial, is that it's also easy to evaluate at half-integers because

𝚪(½) = √π

and we can use the recurrence relation to get exact values for all positive half-integers (or at least, as exact as our value of π).

The third property is less felicitous: there is no easy way to compute 𝚪(z) for arbitrary z to high precision. Unlike the functions discussed above, there is no Taylor series or other trick, no known mechanism for computing the exact value for all arguments. The best we can do is an approximation, perhaps by interpolation between the values that we do know the exact value for.

With that dispiriting setup, we now begin our quest: How best to calculate 𝚪(z) in Ivy?

The first thing I tried was to use a method called the Lanczos approximation, which was described by Cornelius Lanczos in 1964. This gives a reasonable approximate value for 𝚪(z) for a standard floating-point argument. It gives 10-12 decimal digits of accuracy, and a float64 has about 16, float32 about 7. For Ivy we want to do better, but when I uncovered Lanczos's approximation it seemed a good place to start.

Here is the formula:

with

Those c coefficients are the hard part: they are intricate to calculate. Moreover, because this is an approximation, not a series, we can't just compute a few terms and stop. We need to use all the terms of the approximation, which means deciding a priori how many terms to use. Plus, adding more terms does little to improve accuracy, so something like 10 terms is probably enough, given we're not going to be precise anyway. And as we'll see, the number of terms itself goes into the calculation of the c coefficients.

The Wikipedia page for the approximation is a good starting point for grasping all this. It has some sample coefficients and a Python implementation that's easy to relate to the explanation, but using it to calculate the coefficients isn't easy.

I found an article by Paul Godfrey very helpful (Lanczos Implementation of the Gamma Function). It turns the cryptic calculation in the Wikipedia article into a comprehensible burst of matrix algebra. Also, as a step along the way, he gives some sample coefficients for N=11. I used them to implement the approximation using Wikipedia's Python code as a guide, and it worked well. Or as well as it could.

However, if I were going to use those coefficients, it seemed dishonest not to calculate them myself, and Godfrey explains, if not exactly shows, how to do that.

He reduces the calculation of c coefficients to a multiplication of three matrices, D, B, C, and a vector F. I set about calculating them using Ivy itself. I do not claim to understand why the process works, but I am able to execute it.

D is straightforward. In fact its elements are found in my ex-Bell-Labs colleague Neil Sloane's Online Encyclopedia of Integer Sequences as number A002457. The terms are a(n) = (2n+1)!/n!², starting with n=1. Here's the Ivy code to do it (All of these calculations can be found in the Ivy GitHub repo in the file testdata/lanczos). We define the operator to calculate the nth element:

op A2457 n = (!1+2*n)/(!n)**2

The operator is called A2457 for obvious reasons, and it returns the nth element of the sequence. Then D is just a diagonal matrix of those terms, all but the first negated, which can be computed by

N = 6 # The matrix dimension, a small value for illustration here.

op diag v =

d = count v

d d rho flatten v @, d rho 0

The @ decorator iterates its operator, here a comma "raveling" or joining operator, over the elements of its left argument applied to the entire right. The diag operator then builds a vector by spreading out the elements of v with d zeros (d rho 0) between each, then reformats that into a d by d matrix (d d rho ...). That last expression is the return value: operators evaluate to the last expression executed in the body. Here's an example:

diag 1 2 3 4 5 6

1 0 0 0 0 0

0 2 0 0 0 0

0 0 3 0 0 0

0 0 0 4 0 0

0 0 0 0 5 0

0 0 0 0 0 6

For the real work, we pass a vector created by calling A2457 for each of 0 through 4 (-1+iota N-1), negating that, and adding an extra 1 at the beginning. Here's what we get:

D = diag 1, -A2457@ -1+iota N-1

D

1    0    0    0    0    0

0   -1    0    0    0    0

0    0   -6    0    0    0

0    0    0  -30    0    0

0    0    0    0 -140    0

0    0    0    0    0 -630

B is created from a table of binomial coefficients. This turned out to be the most intricate of the matrices to compute, and I won't go through it all here, but briefly: I built Pascal's triangle, put an extra column on it, and rotated it. That built the coefficients. Then I took alternate rows and did a little sign fiddling. The result is an upper triangle matrix with alternating +1 and -1 down the diagonal.

B

 1   1   1   1   1   1

 0  -1   2  -3   4  -5

 0   0   1  -4  10 -20

 0   0   0  -1   6 -21

 0   0   0   0   1  -8

 0   0   0   0   0  -1

Again, if you want to see the calculation, which I'm sure could be done much more concisely, look in the repo.

Now the fun one. The third matrix, C, is built from the coefficients of successive Chebyshev polynomials of the first kind, called Tₙ(x). They are polynomials in x, but we only want the coefficients. That is, x doesn't matter for the value but its presence is necessary to build the polynomials. We can compute the polynomials using these recurrence relations:

T₀(x) = 1

T₁(x) = x

Tₙ₊₁(x) = 2xTₙ(x) - Tₙ₋₁(x)

That's easy to code in Ivy. We treat a polynomial as just a vector of coefficients. Thus, as polynomials, 1 is represented as the vector

1

while x is

0 1

and x² is

0 0 1

and so on. To keep things simple, we always carry around a vector of all the coefficients, even if most are zero. In Ivy we can use the take operator to do this:

6 take 1

1 0 0 0 0 0

gives us a vector of length 6, with 1 as the first element. Similarly, we get the polynomial x by

6 take 0 1

0 1 0 0 0 0

The timesx operator shows why this approach is good. To multiply a polynomial by x, we just push it to the right and add a zero constant at the beginning. But first we should define the size of our polynomials, tsize, which needs to be twice as big as N because, as with the binomials, we will only keep alternate sets of coefficients.

tsize = -1+2*N

op timesx a = tsize take 0, a

That is, put a zero at the beginning of the argument vector and 'take' the first tsize elements of that to be returned.

timesx tsize take 0 1 # makes x²

0 0 1 0 0 0 0 0 0 0 0

And of course to add two polynomials we just add the vectors.

Now we can define our operator T to create the Chebyshev polynomial coefficients.

op T n =

n == 0: tsize take 1

n == 1: tsize take 0 1

(2 * (timesx T n-1)) - (T n-2) # Compare to the recurrence relation.

That T operator is typical Ivy code. The colon operator is a kind of switch/return: If the left operand is true, return the right operand. The code is concise and easy to understand, but can be slow if N is much bigger. (I ended up memoizing the implementation but that's not important here. Again, see the repo for details.) The rest is just recursion with the tools we have built.

To create the actual C matrix, we generate the coefficients and select alternate columns by doubling the argument to T. Finally, for reasons beyond my ken, the first element of the data is hand-patched to 1/2. And then we turn the vector of data into a square N by N matrix:

op gen x = (tsize rho 1 0) sel T 2*x

data =  flatten gen@ -1+iota tsize

data[1] = 1/2

C=N N rho data

C

1/2   0    0    0     0   0

 -1   2    0    0     0   0

  1  -8    8    0     0   0

 -1  18  -48   32     0   0

  1 -32  160 -256   128   0

 -1  50 -400 1120 -1280 512

Phew. Now we just need F, and it's much easier. We need gamma for half-integers, which we know how to do, and then we can calculate some terms as shown in the article.

op gammaHalf n = # n is guaranteed here to be an integer plus 1/2.

n = n - 0.5

(sqrt pi) * (!2*n) / (!n)*4**n

op fn z = ((sqrt 2) / pi) * (gammaHalf(z+.5)) * (**(z+g+.5)) * (z+g+0.5)**-(z+0.5)

F = N 1 rho  fn@ -1+iota N  # N 1 rho ... makes a vertical vector

F

33.8578185471

7.56807943935

3.69514993967

2.34118388428

1.69093653732

1.31989578103

This code will seem like arcana to someone unaccustomed to array languages like APL and Ivy, but Ivy was actually a great tool for this calculation. To be honest, I started to write all this in Go but never finished because it was too cumbersome. The calculation of the C matrix alone took a page of code, plus some clever formatting. In Ivy it's just a few lines and is much more fun.

Now that we have all the pieces, we can do the matrix multiplication that Godfrey devised:

(D+.*B+.*C)+.*F

Those are inner products: +.* means multiply element-wise and then add them up (right to left, remember), standard matrix multiplication. We want the output to have high(ish) precision so print out lots of digits:

'%.22g' text (D+.*B+.*C)+.*F

0.9999999981828222336458

-24.7158058035104436273

-19.21127815952716945532

-2.463474009260883343571

-0.009635981162850649533387

3.228095448247356928485e-05

Using this method, I was able to calculate the coefficients exactly as they appear in Godfrey's article with size N=11. With these coefficients and the code modeled on the Python from Wikipedia, the result was 10 to 12 digits of gamma function.

I was thrilled at first, but the imprecision of the Lanczos approximation, for all its magic, nagged at me. Ivy is supposed to do better than 10 digits, but that's all we can pull out of Lanczos.

After a few days I went back to the web and found another approximation, one by John L. Spouge from 1994, three decades after Lanczos. It has the property that, although it's still only an approximation, the accuracy can be bounded and also tuned at the expense of more computation. That means more terms, but the terms are easy to calculate and the coefficients are much easier to calculate than with Lanczos, so much so that Ivy ends up computing them on demand. We just need a lot more of them.

Even better, I found a paper from 2021 by Matthew F. Causley that refined the approximation further to allow one to decide where the approximation can be most accurate. That paper is The Gamma Function via Interpolation by Matthew F. Causley, 2021.

Let's start with Spouge's original approximation, which looks like this:

where

Notice that the variable a is not only the number of terms, it's also part of the calculations and the coefficients themselves. As in Lanczos, this is not a convergent series but an interpolated approximation. Once you decide on the value of a, you need to use all those terms. (I'll show you some of the coefficients later and you may be surprised at their value.)

The calculation may be long, but it's straightforward given all the groundwork we've laid in Ivy already and those c coefficients are easy to compute.

What Causley adds to this is to separate the number of terms, which he calls N, and the variable based on N that goes into the calculations themselves, which he calls r. In regular Spouge, a=r=N, but Causley splits them. Then, by brute force if necessary, we look for the value of r that gives us the best approximation at some value of z, called zbar, of our choosing. In Causley's paper, he shows his calculated N and optimal r values for a few integer values of zbar. The values in his table are not precise enough for our purposes, however. We need to compute our own.

Here it makes sense to calculate more terms than with Lanczos. Empirically I was able to get about half a digit for every term, and therefore decided to go with N=100, which gives about 50 digits or more, at least near zbar.

The calculation is much simpler than with Lanczos. Given N and r, here's how to calculate the vector of coefficients, cₙ:

op C n =

t = (1 -1)[n&1]/!n

u = e**r-n

v = (r-n)**n+.5

t*u*v

c = N 1 rho (C@ iota N)

Once we have those coefficients, the gamma function itself is just the formula:

op gamma z =

p = (z+r)**z-.5

q = **-(z+r)

n = 0

sum = cinf

:while n <= N-1

sum = sum+c[n]/(z+n)

n = n+1

:end

p*q*sum

The variable cinf is straight from the paper. It appears to be a fixed value.

cinf = 2.5066 # Fixed by the algorithm; see Causley.

I ended up with N=100 and r=126.69 for zbar=6. Let's see how accurate we are.

)format %.70f # The number of digits for a 256-bit mantissa, not counting the 8 left of the decimal sign.

gamma 12

39916799.9999999999999999999999999999999999999999083377203094662100418136867266

The correct value is !11, which is of course an integer (and computed as such in Ivy):

!11

39916800

They agree to 48 places, a huge step up from Lanczos and a difference unlikely to be noticed in normal work.

Have a gander at the first few of our cₙ coefficients with N=11 and r=126.69:

)format %.12e

c

 1.180698687310e+56

-5.437816144514e+57

 1.232332820715e+59

-1.831910616577e+60

 2.009185300215e+61

-1.733868504749e+62

 1.226116937711e+63

...

They have many more digits than that, of course, but check out the exponents. We are working with numbers of enormous size; it's remarkable that they almost completely cancel out and give us our gamma function with such accuracy. This is indeed no Taylor series.

I chose N because I wanted good accuracy. I chose r because it gave me excellent accuracy at gamma 6 and thereabouts, well over 50 digits. To find my value of r, I just iterated, computing C and then gamma using values of r until the error between gamma 6 and !5 was as small as I could get. It's explained in the repo in the file testdata/gamma.

But there remains one mystery. In Causley's paper, r is closer to N, in fact always less than one away. So why did I end up with such a different value? The result I get with those parameters is excellent, so I am not complaining. I am just puzzled.

The optimization method is outlined in Causley's paper but not thorougly enough for me to recreate it, so I did something simpleminded: I just varied r until it gave good results at zbar=6. Perhaps that's naive. Or perhaps there is a difference in our arithmetical representation. Causley says he uses variable-precision arithmetic but does not quantify that. I used 256-bit mantissas. It's possible that the highest-precision part of the calculations is exquisitely sensitive to the size of the mantissa. I don't know, and would like to know, what's going on here. But there is no question that my values work well. Moreover, if I instead choose r=N, as in the original paper by Spouge, the answer has 38 good digits, which is less than in my version but also much more than a 64-bit float could deliver and perhaps more than Causley's technique could capture. (I do not mean to impugn Causley here! I just don't know exactly how he computed his values.)

However that may play out, there may be only one person who cares about the accuracy of the gamma function in Ivy. And that person thoroughly enjoyed exploring the topic and building a high-resolution, if necessarily imperfect, implementation.

Thanks for reading. If you want to try Ivy,

    go install robpike.io/ivy@latest

 

On Bloat

The link below holds the slides from a talk I gave last year for the Commonwealth Bank of Australia's annual tech conference. They are mostly self-explanatory, with the possible exception of the "attractive nuisance" slide, for which I explained how a small package with good intentions can accumulate both a large set of dependents and a large set of dependencies, turning it into a vector for bloat and malfeasance.

Click here: On Bloat

What We Got Right, What We Got Wrong

 

This is my closing talk (video) from the GopherConAU conference in Sydney, given November 10, 2023, the 14th anniversary of Go being launched as an open source project. The text is interspersed with the slides used in the presentation.

What We Got Right, What We Got Wrong

INTRODUCTION

Hello.

Let me start by thanking Katie and Chewy for the giving me the honor of presenting the closing talk for the conference. And apologize for reading this from my script but I want to get the words right.

November 10, 2009

Today is November 10, 2023, the 14th anniversary of the launch of Go as an open source project.

That day, at 3pm California time if memory serves, Ken Thompson, Robert Griesemer, Russ Cox, Ian Taylor, Adam Langley, Jini Kim and I watched expectantly as the site went live and the world learned what we had been up to.

Fourteen years later, there is much to look back on. Today I'd like to take the opportunity to talk about some of the larger lessons learned since that day. Even the most successful projects have things that, upon reflection, could have been done better. And of course, things that in hindsight seem to have been key to their success.

Up front I must make clear that I am speaking only for myself, not for the Go team and not for Google.  Go was and still is a huge effort by a dedicated team and a huge community, so if you agree with anything I say, thank them. If you disagree, blame me but please keep it to yourself 😃.

Given the title of this talk, many people might expect I'm going to be analyzing good and bad things in the language. Of course I'll do some of that, but much more besides, for several reasons.

First, what's good and bad in a programming language is largely a matter of opinion rather than fact, despite the certainty with which many people argue about even the most trivial features of Go or any other language.

Also, there has already been plenty of discussion about things such as where the newlines go, how nil works, using upper case for export, garbage collection, error handling, and so on.  There are certainly things to say there, but little that hasn't already been said.

But the real reason I'm going to talk about more than the language is that that's not what the whole project was about. Our original goal was not to create a new programming language, it was to create a better way to write software. We had issues with the languages we were using—everyone does, whatever the language—but the fundamental problems we had were not central to the features of those languages, but rather to the process that had been created for using them to build software at Google.

The first gopher on a t-shirt

The creation of a new language provided a new path to explore other ideas, but it was only an enabler, not the real point. If it didn't take 45 minutes to build the binary I was working on at the time, Go would not have happened, but those 45 minutes were not because the compiler was slow, because it wasn't, or because the language it was written in was bad, because it wasn't. The slowness arose from other factors.

And those factors were what we wanted to address: The complexities of building modern server software: controlling dependencies, programming with large teams with changing personnel, ease of maintainability, efficient testing, effective use of multicore CPUs and networking, and so on.

In short, Go is not just a programming language. Of course it is a programming language, that's its definition, but its purpose was to help provide a better way to develop high-quality software, at least compared to our environment 14 plus years ago.

And that's still what it's about today. Go is a project to make building production software easier and more productive.

A few weeks back, when starting to prepare this talk, I had a title but little else.  To get me going, I asked people on Mastodon for input. A fair few responded, and I noticed a trend in the replies: people thought the things we got wrong were all in the language, but those we got right were in the larger story, the stuff around the language like gofmt and deployment and testing. I find that encouraging, actually. What we were trying to do seems to have had an effect.

But it's worth admitting that we didn't make clear early on what the true goals were. Perhaps we felt they were self-evident.  To address that shortcoming, in 2013 I gave a talk at the SPLASH conference entitled, Go at Google: Language Design in the Service of Software Engineering.

Go at Google

That talk and associated blog post are perhaps the best explanation of why Go happened.

Today's talk is something of a follow-on to the SPLASH talk, looking back on the lessons learned once we got past building the language and could apply ourselves to the bigger picture more broadly.

And so... some lessons.

First, of course, we have:

The Gopher

It may seem an odd place to start, but the Go gopher is one of the earliest factors in Go's success.  We knew long before the launch that we wanted a mascot to adorn the schwag - every project needs schwag - and Renee French offered to create one for us. We got that part absolutely right.

Here is a picture of the very first instance of the gopher plushie.

The gopher

And here is a picture of the gopher with the less successful first prototype.

The gopher with his less evolved ancestor

The Gopher is a mascot who serves as a badge of honor, even an identifier for Go programmers everywhere.  At this moment you are in a conference, one of many, called GopherCon.  Having a recognizable, funny creature ready to share the message from day one was vital to Go's growth.  Its goofy yet intelligent demeanor—he can build anything!

Gophers building a robot (drawing by Renee French)

—sets the tone for the community's engagement with the project, one of technical excellence allied with real fun. Most important, the gopher serves as a banner for the community, a flag to rally around, especially in the early days when Go was still an upstart in the programming world.

Here's a picture of gophers attending a conference in Paris some years back. Look how excited they are!

Gopher audience in Paris (photo by Brad Fitzpatrick)

All that said, releasing the Gopher design under a Creative Commons Attribution license was perhaps not the best choice.  On the one hand, it encouraged people to remix him in fun ways, which in turn helped foster community spirit.

Gopher model sheet

Renee created a "model sheet" to help artists work with him while keeping him true to his spirit.

Some artists had fun playing with these characteristics and making their own versions of him; Renee and my favorites are the ones by the Japanese designer @tottie:

@tottie's gophers

and game programmer @tenntenn:

@tenntenn's gopher

But the "attribution" part of the license often resulted in frustrating arguments, or in false credit given to Renee for creations that were not hers and not in the spirit of the original. And, to be honest, the attribution was often honored only reluctantly or not at all. For instance, I doubt @tenntenn was compensated or even acknowledged for this use of his gopher illustration.

gophervans.com: Boo!

So if we were doing it over, we'd think hard about the best way to make sure the mascot stays true to his ideals. It's a hard problem, maintaining a mascot, and the solution remains elusive.

But on to more technical things.

Done Right

Here is a list of things that I think we got objectively right, especially in retrospect.  Not every language project has done these things, but each was crucial to the ultimate success of Go. I'll try to be brief, because they will all be familiar topics.

1. Specification. We started with a formal specification. Not only does that lock down behavior when writing a compiler, it enables multiple implementations to coexist and agree on that behavior. A compiler alone is not a specification. What do you test the compiler against?

The specification, as seen on the web

Oh and by the way, the first draft of the specification was written here, on the 18th floor of a building on Darling Harbour in Sydney. We are celebrating Go's birthday in Go's home town.

2. Multiple implementations. There are multiple compilers, all implementing the same spec. Having a spec makes this much easier to achieve.

Ian Taylor surprised us when he sent mail one day informing us that, having read our draft spec, he'd written a compiler himself.

    Subject: A gcc frontend for Go

    From: Ian Lance Taylor

    Date: Sat, Jun 7, 2008 at 7:06 PM

    To: Robert Griesemer, Rob Pike, Ken Thompson

    One of my office-mates pointed me at http://.../go_lang.html .  It

    seems like an interesting language, and I threw together a gcc

    frontend for it.  It's missing a lot of features, of course, but it

    does compile the prime sieve code on the web page.

That was mind-blowing, but many more have followed, all made possible by the existence of a formal specification.

Lots of compilers

Having multiple compilers helped us refine the language and polish the specification, as well as providing an alternative environment for others less enamored with our Plan-9-like way of doing business.

(More about that later.)

Today there are lots of compatible implementations, and that's great.

3. Portability. We made cross-compilation trivial, which allowed

programmers to work on whatever platform they liked, and ship to whatever platform was required. This may be easier with Go than with any other language.  It's easy to think of the compiler as

native to the machine it runs on, but it has no reason to be.

Breaking that assumption is powerful and was news to many developers.

Portability

4. Compatibility. We worked hard to get the language in shape for

version 1.0, and then locked it down with a compatibility guarantee. Given what a dramatic, documented effect that made on Go's uptake, I find it puzzling that most other projects have resisted doing this.  Yes, there's a cost in maintaining strong compatibility, but it blocks feature- itis and, in a world in which almost nothing else is stable, it's delightful not to have to worry about new Go releases breaking your project.

The Go compatibility promise

5. The library. Although it grew somewhat as an accident, as there was no other place to install Go code at the beginning, the existence of a solid, well-made library with most of what one needed to write 21st century server code was a major asset. It kept the community all working with the same toolkit until we had experience enough to understand what else should be made available. This worked out really well and helped prevent variant libraries from arising, helping unify the community.

The library

6. Tools. We made sure the language was easy to parse, which enabled tool-building. At first we thought we'd need an IDE for Go, but easy tooling meant that, in time, the IDEs would come to Go. And along with gopls, they have, and they're awesome.

Tools

We also provided a set of ancillary tools with the compiler, such as automated testing, coverage, and code vetting. And of course the go command, which integrated the whole build process and is all many projects need to build and maintain their Go code.

Fast builds

Also, it didn't hurt that Go acquired a reputation for fast builds.

7. Gofmt. I pull gofmt out as a separate item from tools because it is the tool that made a mark not only on Go, but on the programming community at large. Before Robert wrote gofmt (which, by the way, he insisted on doing from the very beginning), automated formatters were not high quality and therefore mostly unused.

Gofmt proverb

Gofmt showed it could be done well, and today pretty much every language worth using has a standard formatter. The time saved by not arguing over spaces and newlines is worth all the time spent defining a standard format and writing this rather difficult piece of code to automate it.

Also, gofmt made countless other tools possible, such as simplifiers, analyzers and even the code coverage tool. Because gofmt's guts became a library anyone could use, you could parse a program, edit the AST, and just print byte-perfect output ready for humans to use as well as machines.

Thanks, Robert.

Enough with the congratulations, though. On to some more contentious topics.

Concurrency

Concurrency is contentious? Well, it certainly was in 2002, the year I joined Google. John Ousterhout had famously written that threads were bad, and many people agreed with him because they seemed to be very hard to use.

John Ousterhout doesn't like threads

Google software avoided them almost always, pretty much banning them outright, and the engineers doing the banning cited Ousterhout. This bothered me. I'd been doing concurrency-like things, sometimes without even realizing it, since the 1970s and it seemed powerful to me. But upon reflection it became clear that Ousterhout was making two mistakes. First, he was generalizing beyond the domain he was interested in using threads for, and second, he was mostly complaining about using them through with clumsy low-level packages like pthread, and not about the fundamental idea.

It's a mistake common to engineers everywhere to confuse the solution and the problem like this. Sometimes the proposed solution is harder than the problem it addresses, and it can be hard to see there is an easier path. But I digress.

I knew from experience that there were nicer ways to use threads, or whatever we choose to call them, and even gave a pre-Go talk about them.

Concurrency in Newsqueak

But I wasn't alone in knowing this; a number of other languages, papers, and even books had been written about concurrent programming that showed it could be done well. It just hadn't caught on as a mainstream idea yet, and Go was born partly to address that. In that legendary 45-minute build I was trying to add a thread to a non-threaded binary, and it was frustratingly hard because we were using the wrong tools.

Looking back, I think it's fair to say that Go had a significant role in convincing the programming world that concurrency was a powerful tool, especially in the multicore networked world, and that it could be done better than with pthreads. Nowadays most mainstream languages have good support for concurrency.

Google 3.0

Also, Go's version of concurrency was somewhat novel, at least in the line of languages that led to it, by making goroutines unflavored.  No coroutines, no tasks, no threads, no names, just goroutines. We invented the word "goroutine" because no existing term fit. And to this day I wish the Unix spell command would learn it.

As an aside, because I am often asked about it, let me speak for a minute about async/await.  It saddens me a bit that the async/await model with its associated style is the way many languages have chosen to support concurrency, but it is definitely a huge improvement over pthreads.

Compared to goroutines, channels, and select, async/await is easier and smaller for language implementers to build or to retrofit into existing platforms. But it pushes some of the complexity back on the programmer, often resulting in what Bob Nystrom has famously called "colored functions".

What Color is Your Function?

I think Go shows that CSP, which is a different but older model, fits perfectly into a procedural language without such complication. I've even seen it done several times as a library. But its implementation, done well, requires a significant runtime complexity, and I can understand why some folks would prefer not to build that into their system. It's important, though, whatever concurrency model you provide, to do it exactly once, because an environment providing multiple concurrency implementations can be problematic. Go of course solved that issue by putting it in the language, not a library.

There's probably a whole talk to give about these matters, but that's enough for now.

[End of aside]

Another value of concurrency was that it made Go seem like something new.  As I said, some other languages had supported it before, but they were never mainstream, and Go's support for concurrency was a major attractor that helped grow early adoption, pulling in programmers that hadn't used concurrency before but were intrigued by its possibilities.

And that's where we made two significant mistakes.

Whispering gophers (Cooperating Sequential Processes)

First, concurrency is fun and we were delighted to have it, but the use cases we had in mind

were mostly server stuff, meant to be done in key libraries such as net/http, and not everywhere in every program.  And so when many programmers played with it, they struggled to work out how it really helped them.  We should have explained up front that what concurrency support in the language really brought to the table was simpler server software.  That problem space mattered to many but not to everyone who tried Go, and that lack of guidance is on us.

The related second point is that we took too long to clarify the difference between parallelism - supporting multiple computations in parallel on a multicore machine - and concurrency, which is a way to structure code to do that well.

Concurrency is not parallelism

Countless programmers tried to make their code faster by parallelizing it using goroutines, and were often baffled by the resulting slowdown. Concurrent code only goes faster when parallelized if the underlying problem is intrinsically parallel, like serving HTTP requests. We did a terrible job explaining that, and the result baffled many programmers and probably drove some away.

To address this, in 2012 I gave a talk at Waza, Heroku's developer conference, called, Concurrency is not Parallelism. It's a fun talk but it should have happened earlier.

Apologies for that. But the good point still stands: Go helped popularize concurrency as a way to structure server software.

Interfaces

It's clear that interfaces are, with concurrency, a distinguishing idea in Go. They are Go's answer to objected-oriented design, in the original, behavior-focused style, despite a continuing push by newcomers to make structs carry that load.

Making interfaces dynamic, with no need to announce ahead of time which types implement them, bothered some early critics, and still irritates a few, but it's important to the style of programming that Go fostered.  Much of the standard library is built upon their foundation, and broader subjects such as testing and managing dependencies rely heavily on their generous, "all are welcome" nature.

I feel that interfaces are one of the best-designed things in Go.

Other than a few early conversations about whether data should be included in their definition, they arrived fully formed on literally the first day of discussions.

A GIF decoder: an exercise in Go interfaces (Rob Pike and Nigel Tao 2011)

And there is a story to tell there.

On that famous first day in Robert's and my office, we asked the question of what to do about polymorphism. Ken and I knew from C that qsort could serve as a difficult test case, so the three of us started to talk about how our embryonic language could implement a type-safe sort routine.

Robert and I came up with the same idea pretty much simultaneously: using methods on types to provide the operations that sort needed. That notion quickly grew into the idea that value types had behaviors, defined as methods, and that sets of methods could provide interfaces that functions could operate on. Go's interfaces arose pretty much right away.

sort.Interface

That's something that is not often not acknowledged: Go's sort is implemented as a function that operates on an interface. This is not the style of object-oriented programming most people were familiar with, but it's a very powerful idea.

That idea was exciting for us, and the possibility that this could become a foundational

programming construct was intoxicating.  When Russ joined, he soon pointed out how I/O would fit beautifully into this idea, and the library took place rapidly, based in large part on the three famous interfaces: empty, Writer, and Reader, holding an average of two thirds of a method each.  Those tiny methods are idiomatic to Go, and ubiquitous.

The way interfaces work became not only a distinguishing feature of Go, they became the way we thought about libraries, and generality, and composition. It was heady stuff.

But we might have erred in stopping the conversation there.

You see, we went down this path at least in part because we had seen too often how generic programming encouraged a way of thinking that tended to focus on types before algorithms. Early abstraction instead of organic design. Containers instead of functions.

We defined generic containers in the language proper - maps, slices, arrays, channels - without giving programmers access to the genericity they contained. This was arguably a mistake. We believed, correctly I still think, that most simple programming tasks could be handled just fine by those types. But there are some that cannot, and the barrier between what the language provided and what the user could control definitely bothered some people.

In short, although I wouldn't change a thing about how interfaces worked, they colored our thinking in ways it took more than a decade to correct. Ian Taylor pushed us, from early on, to face this problem, but it was quite hard to do given the presence of interfaces as the bedrock of Go programming.

Critics often complained we should just do generics, because they are "easy", and perhaps they can be in some languages, but the existence of interfaces meant that any new form of polymorphism had to take them into account. Finding a way forward that worked well with the rest of the language required multiple attempts, several aborted implementations, and many hours, days, and weeks of discussion. Eventually we roped in some type theorists to help out, led by Phil Wadler.  And even today, with a solid generic model in the language, there are still lingering problems to do with the presence of interfaces as method sets.

Generic sort specification

The final answer, as you know, was to design a generalization of interfaces that could absorb more forms of polymorphism, transitioning from "sets of methods" to "sets of types". It's a subtle but profound move, one that most of the community seems to be fine with, although I suspect the grumbling will never stop.

Sometimes it takes many years to figure something out, or even to figure out that you can't quite figure it out. But you press on.

By the way, I wish we had a better term than "generics", which originated as the term for a different, data-structure-centric style of polymorphism. "Parametric polymorphism" is the proper term for what Go provides, and it's an accurate one, but it's an ugly mouthful. But "generics" is what we say, even though it's not quite right.

The Compiler

One of the things that bothered the programming language community was that the early Go compiler was written in C. The proper way, in their opinion, was to use LLVM or a similar toolkit, or to write the compiler in Go itself, a process called self-hosting.  We didn't do either of these, for several reasons.

First, bootstrapping a new language requires that at least the first steps towards its compiler must be done in an existing language. For us, C was the obvious choice, as Ken had written a C compiler already, and its internals could serve well as the basis of a Go compiler. Also, writing a compiler in its own language, while simultaneously developing the language, tends to result in a language that is good for writing compilers, but that was not the kind of language we were after.

The early compiler worked. It bootstrapped the language well. But it was a bit of an odd duck, in effect a Plan 9-style compiler using old ideas in compiler writing, rather than new ones such as static single assignment.  The generated code was mediocre, and the internals were not pretty.  But it was pragmatic and efficient, and the compiler code itself was modest in size and familiar to us, which made it easy to make changes quickly as we tried new ideas. One critical step was the addition of segmented stacks that grew automatically. This was very easy to add to our compiler, but had we been using a toolkit like LLVM, the task of integrating that change into the full compiler suite would have been infeasible, given the required changes to the ABI and garbage collector support.

Another area that worked well was cross-compilation, which came directly from the way the original Plan 9 compiler suite worked.

Doing it our way, however unorthodox, helped us move fast. Some people were offended by this choice, but it was the right one for us at the time.

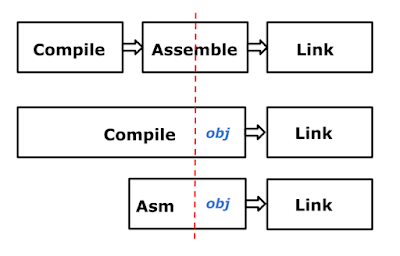The Go compiler architecture post Go 1.5

For Go version 1.5, Russ wrote a tool to translate the compiler semi-automatically from C to Go. By then the language was complete, and concerns about compiler-directed language design were irrelevant. There are talks online about this process that are worth a look. I gave one talk at GopherCon in 2016 about the assembler, which is something of a high point in my lifelong quest for portability.

The Design of the Go Assembler (GopherCon 2016)

We did the right thing by starting in C, but eventually translating the compiler to Go has allowed us to bring to its development all the advantages that Go has, including testing, tooling, automatic rewriting, performance analysis, and so on. The current compiler is much cleaner than the original and generates much better code. But, of course, that is how bootstrapping works.

Remember, our goal was just not a language, but much more.

Our unusual approach was in no way an insult to LLVM or anyone in the language community. We just used the tool that best suited our task. And of course, today there is an LLVM-hosted compiler for Go, and many others, as there should be.

Project Management

We knew from the start that to succeed, Go had to be an open source project. But we also knew that it would be more productive to develop in private until we had the key ideas figured out and a working implementation. Those first two years were essential to clarifying, free of distraction, what we were trying to achieve.

The transition to open source was a huge change, and educational. The input from the community was overwhelming. Engaging with the community took a lot of time and effort, especially for Ian, who somehow found time to answer every question anyone asked. But it also brought so much more. I still marvel at how quickly the Windows port arrived, done entirely by the community under the guidance of Alex Brainman. That was amazing.

It took us a long time to understand the implications of the switch to an open source project, and how to manage it.

In particular, it's fair to say it took us too long to understand the best way to work with the community. A theme throughout this talk is poor communication on our part - even as we thought we were communicating well - and a lot of time was wasted due to misunderstandings and mismatched expectations. It could have been better done.

In time, though, we convinced the community, at least the part that stayed with us, that some of our ideas, although different from the usual open source way, were valuable. The most important were around our insistence on maintaining high code quality through mandatory code review and exhaustive attention to detail.

Mission Control (drawing by Renee French)

Some projects work differently, accepting code quickly and then cleaning up once it's been committed. The Go project works the other way around, trying to get the quality first. I believe that's the more efficient way, but it pushes more work back on the community and they need to understand the value or they will not feel as welcome as they should. There is still much to learn here, but I believe things are much better these days.

By the way, there's a historical detail that's not widely known. The project has had 4 different content management systems: SVN, Perforce, Mercurial and then Git. Russ did a Herculean job of keeping all the history alive, so even today the Git repo contains the earliest changes as they were made in SVN. We all believe it's valuable to keep the history around, and I thank him for doing the heavy lifting.

One other point. People often assume Google tells the Go team what to do. That's simply not true. Google is incredibly generous in its support for Go, but does not set the agenda. The community has far more input. Google has a huge internal Go code base that the team uses to test and verify releases, but this is done by importing from the public repo into Google, not the other way around. In short, the core Go team is paid by Google but they are independent.

Package Management

The process of developing package management for Go was not done well. The package design in the language itself was excellent, I believe, and consumed a large amount of time in the first year or so of our discussions. The SPLASH talk I mentioned earlier explains in detail why it works the way it does if you're interested.

A key point was the use of a plain string to specify the path in an import statement, giving a flexibility that we were correct in believing would be important. But the transition from having only a "standard library" to importing code from the web was bumpy.

Fixing the cloud (drawing by Renee French)

There were two issues.

First, those of us on the core Go team early on were familiar with how Google worked, with its monorepo and everyone building at head. But we didn't have enough experience using a package manager with lots of versions of packages and the very difficult problems trying to resolve the dependency graph. To this day, few people really understand the technical complexities, but that is no excuse for our failure to grapple with those problems from the start. It's especially embarrassing because I had been the tech lead on a failed project to do something similar for Google's internal build, and I should have realized what we were up against.

deps.dev

My work on deps.dev was a something of a penance.

Second, the business of engaging the community to help solve the dependency management problem was well-intentioned, but when the final design came out, even with plenty of documentation and writing about the theory, many in the community felt slighted.

pkg.go.dev

This failing was a lesson to the team in how engagement with the community should really work, and much has improved since as a result.

Things are settled now, though, and the design that emerged is technically excellent and appears to be working well for most users. It just took too long and the road was bumpy.

Documentation and Examples

Another thing we didn't get right up front was the documentation. We wrote a lot of it, and thought we did a good job, but it soon became clear that the community wanted a different level of documentation than we expected.

Gophers fixing a Turing machine (drawing by Renee French)

The key missing piece was examples of even the simplest functions. We thought that all you needed to do was say what something did; it took us too long to accept that showing how to use it was even more valuable.

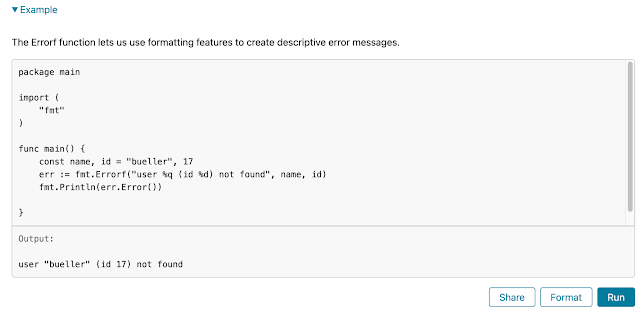Executable examples

That lesson was learned, though. There are plenty of examples in the documentation now, mostly provided by open source contributors. And one thing we did very early was make them executable on the web. I gave a talk at Google I/O in 2012 that showed concurrency in action, and Andrew Gerrand wrote a lovely bit of web goo that made it possible to run the snippets right from the browser. I doubt that was the first time it had ever been done, but Go is a compiled language and many in the audience had never seen that trick before. The technology was then deployed to the blog and to the online package documentation.

The Go playground

Perhaps even more important was its deployment to the Go playground, a freely available open sandbox for people to try things out, and even develop code.

Conclusion

We have come a long way.

Looking back, it's clear many things were done right, and they all helped Go succeed. But much could have been done better, and it's important to own up to those and learn from them. There are lessons on both sides for anyone hosting a significant open source project.

I hope that my historical tour of the lessons and their causes will be helpful, and perhaps serve as a sort of apology/explanation for those who objected to what we were doing and how we were doing it.

GopherConAU 2023 mascot by Renee French

But here we are, 14 years after the launch. And it's fair to say that overall it's a pretty good place.

Largely because of the decisions made through the design and development of Go as a way to write software - not just as a programming language - we have arrived somewhere novel.

We got here in part because of:

• a strong standard library that implements most of the basics needed for server code
• concurrency as a first-class component of the language
• an approach based on composition rather than inheritance
• a packaging model that clarifies dependency management
• integrated fast build and testing tools
• rigorous consistent formatting
• a focus on readability over cleverness
• a compatibility guarantee

And, most of all, because of the support of an unbelievably helpful and diverse community of Gophers.

A diverse community (drawings by @tenntenn)

Perhaps the most interesting consequence of these matters is that Go code looks and works the same regardless of who's writing it, is largely free of factions using different subsets of the language, and is guaranteed to continue to compile and run as time goes on. That may be a first for a major programming language.

We definitely got that right.

Thank you.